排序算法小笔记

~~接上级要求（bushi~~

最近开始玩算法了，自己胡乱在力扣上刷了一两周题，没有啥方向和规划可言。恰逢导师@Uni准备重构自己的算法知识体系，于是就顺便把我捎上了。这一周的任务是初步了解一些排序算法，不过在开始之前还要做一些小准备。

0.稳定排序&不稳定排序

所谓稳定的定义，就是假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，A1=A2，且A1在A2之前，而在排序后的序列中，A1仍在A2之前，则称这种排序算法是稳定的；否则称为不稳定的。

了解了这个，我们就可以开始基本的研究了。

1.冒泡排序 Bubble sort

冒泡排序应该是比较耳熟能详的一个排序算法了，大一的时候上C语言课中就有用过。

冒泡的思想主要是通过逐个比较将大的数往后放，将小的数往前移。算法有两个内外两个循环，内层循环每循环一次都可以将当前范围内最大的数放到最后，实现“冒泡”。因为比较简单，就直接上代码吧

for (int i = 0; i < len - 1; i++)
    for (int j = 0; j < len - 1 - i; j++)
        if (arr[j] > arr[j + 1])
        {
            int temp = arr[j];
            arr[j] = arr[j + 1];
            arr[j + 1] = temp;
        }

很容易看出来，这是稳定排序的一种。两个数字不一样大小的时候才会移动，相同大小的数字是不会改变彼此的相对位置的。

2.选择排序 Selection sort

一句话来讲排序数组就是：每次将待排序数组中最小的那个拿出来。

from runoob

他和冒泡排序相比，都是内外嵌，但是选择排序不需要每次都对两个数字进行交换，而是只需要对当前循环的第一个数和当前循环的最小数交换即可。

for (int i = 0; i < arr.size() - 1; i++) {
    int min = i;//用于记录最小数的下标
    for (int j = i + 1; j < arr.size(); j++)
        if (arr[j] < arr[min])
               min = j;
    std::swap(arr[i], arr[min]);//交换
}

也很容易看出来，这是一个稳定排序。

选择排序与冒泡排序的排序过程恰好是相反的，前者是将小数挪前，后者是将大数置后。

3.插入排序

插入排序开始，思想上就没有那么简单粗暴了，不过也很好理解。其原理也可以一句话讲得明白：在已排序数组中找到未排序数该插入的位置。

啥意思呢？还是先来看一段动图

假设数组前的n位都已经排好了序，那么第n+1想要插进来，就要找到在前n位中他应该插入的位置。代码实现如下：

for(int i=1;i<len;i++){
    int key=arr[i]; // 当前要往前插入的数字
    int j=i-1; //前面以及排好序的j个数的末尾坐标
    while((j>=0) && (key<arr[j])){ //开始遍历寻找插入位置
        arr[j+1]=arr[j]; //还没找到，往后挪
        j--;
    }
    arr[j+1]=key; //找到了，插入
}

同样可以看出来，这也是一个稳定排序，在寻找插入位置的时候，遇到相同大小的数，会插入到其后面，也是不会改变相同元素的相对位置。

4.归并排序

归并排序是这次遇到的一个比较复杂的排序算法，它用到了分治的思想。先将原本的数组分解成数个子数组，对子数组排序后再合并回去，得到最终的排序后数组。还是通过动图来感受一下并归排序的实现过程

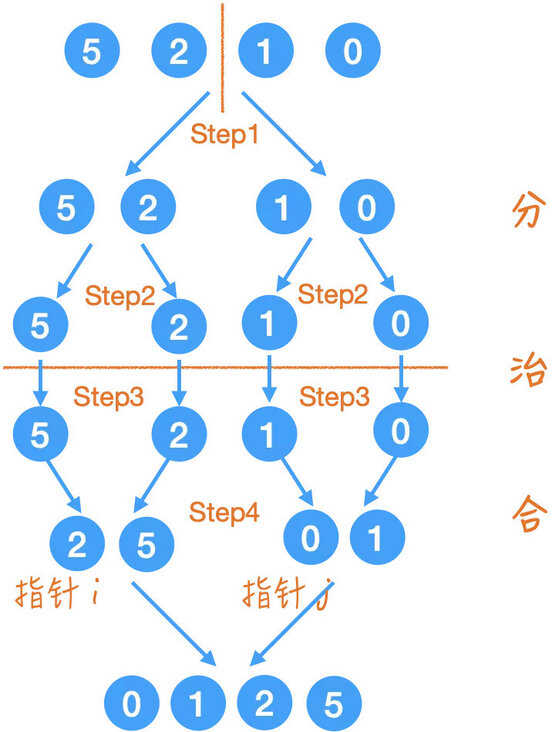
我们将数组逐步拆分（就像遇到大问题的时候将大问题逐渐化简为一个个小问题），直到最小单位，也就是一个数的时候。这个时候，逐层将所有数组合并起来，并且在合并的时候就顺便进行了排序。具体是什么情况呢？

以上图为例，从step3开始，左边的[5]与[2]两个单元素数组合并，右边的[1]和[0]两个单元素数组合并，插入新的数组之前先比较，5>2所以先插入2再插入5，右边同理得到[0,1]。

然后是[2,5]与[0,1]合并，因为两个数组都是已经排好序了的，处理起来就方便得多，用i作为第一个数组的指针，[j]作为第二个数组的指针，先看当i=0, j=0时，对分别对两指针对应的值比较，即2和0，先插入0，此时j++，而i保持不变。这个时候i=0, j=1，再次比较两指针对应的值，即2和1，先插入1，此时还是j++，i不变，以此类推，实现按照合并的同时保持升序。伪代码实现如下

int i = 0, j = 0, k = 0;
while(i < arr1.size() && j < arr2.size()) {
    if (arr1[i] <= arr2[j])
        arr[k++] = arr1[i++];
    else
        arr[k++] = arr2[j++];
}

while(i < arr1.size()) arr[k++] = arr1[i++];
while(j < arr2.size()) arr[k++] = arr2[j++];

道理我都懂，你的step1, step2又要怎么做呢？其实这里可以用到一个递归的思想，上一段代码就好

void merge(vector<int>& arr, vector<int>& temp, int left, int right) {
    if (left >= right) return;
    int mid = left + (right - left) / 2;
    
    //递归拆分
    merge_sort(arr, temp, left, mid);
    merge_sort(arr, temp, mid + 1, right);

    for(int i = left;i<=right;i++) 
        temp[i] = arr[i];
}

可以看出来，我们说要拆分数组，并不是真的每次再开一个额外的数组空间去存储我们分割开的子元素，而是用left和right两个“指针”（或者称为“挡板”）来将子数组“框”住。让我们的操作只在这一个范围内，从而实现一个“子数组”。

将我们上面的思路整合一下，归并排序的代码已经呼之欲出了

#include <bits/stdc++.h>
using namespace std;

void merge_sort(vector<int>& arr, vector<int>& temp, int left, int right) {
    if (left >= right) return;
    int mid = left + (right - left) / 2;
    
    //分治
    merge_sort(arr, temp, left, mid);
    merge_sort(arr, temp, mid + 1, right);

    for(int i = left;i<=right;i++) 
        temp[i] = arr[i];

    //合
    int i = left, j = mid + 1, k = left;
    while(i <= mid && j <= right) {
        if (temp[i] <= temp[j])
            arr[k++] = temp[i++];
        else
            arr[k++] = temp[j++];
    }

    while(i <= mid)
        arr[k++] = temp[i++];

    while(j <= right)
        arr[k++] = temp[j++];
}

void merge_sort(vector<int>& arr) {
    vector<int> temp(arr.size());
    merge_sort(arr, temp, 0, arr.size() - 1);
}

int main()
{
    vector<int> arr = { 0,2,3,2,1,11,5,8,4,2 };
    merge_sort(arr);
    vector<int>::iterator it = arr.begin();
    while (it != arr.end()) {
        cout << *it << " ";
        it++;
    }
    cout << endl;
    return 0;
}

那么这个归并排序的稳定性如何呢？关键就在于我们比较的时候，也就是这个地方

while(i <= mid && j <= right) {
    if (temp[i] <= temp[j]) //这里！
        arr[k++] = temp[i++];
    else
        arr[k++] = temp[j++];
}

可以看出来，当遇到相等数组的时候，会保持原有相对顺序，优先插入左侧“子数组”的元素。所以归并排序的算法也是稳定排序。

小结

到这里，这次的基础排序算法了解就到这里了。一次四个，刚好吃到八分饱，留几个下次吃。

顺便附上个几个常见排序的复杂度情况。

查阅资料：

三叶の小窝

排序算法小笔记